Diagramas de cuerpo libre
4.1.
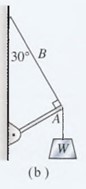
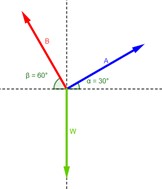
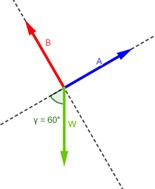
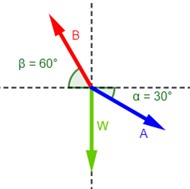
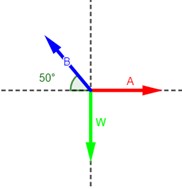
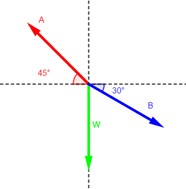
Dibuje un diagrama de cuerpo libre correspondiente a las situaciones ilustradas en la figura 4.19a y b. Descubra un punto en el cual actúen las fuerzas importantes y represente cada fuerza como un vector. Calcule el ángulo de referencia y escriba los nombres de las componentes.


4.2.
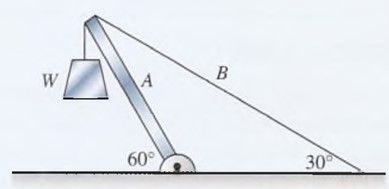
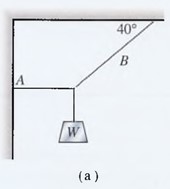
Estudie cada una de las fuerzas que actúan en el extremo de la viga ligera de la figura 4.20.
Dibuje el diagrama de cuerpo libre apropiado.
Solución de problemas de equilibrio
4.3.
Tres ladrillos idénticos están atados entre sí por medio de cuerdas y penden de una balanza que marca en total 24 N. ¿Cuál es la tensión de la cuerda que sostiene al ladrillo inferior?, ¿Cuál es la tensión en la cuerda que se encuentra entre el ladrillo de en medio y el ladrillo superior? R= 8 N, 16 N
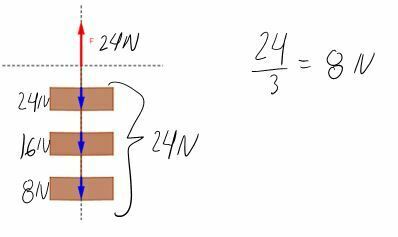
4.4.
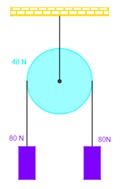
Una sola cadena sostiene una polea que pesa 40 N. Entonces se conectan dos pesas idénticas de 80 N con una cuerda que pasa por la polea. ¿Cuál es la tensión en la cadena que sostiene todo el conjunto? ¿Cuál es la tensión en cada cuerda? R= 200N, cada cuerda soporta 80 N.

4.5.
Si el bloque de la figura 4.19a pesa 80 N, ¿cuáles son las tensiones en las cuerdas A y B?
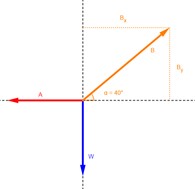
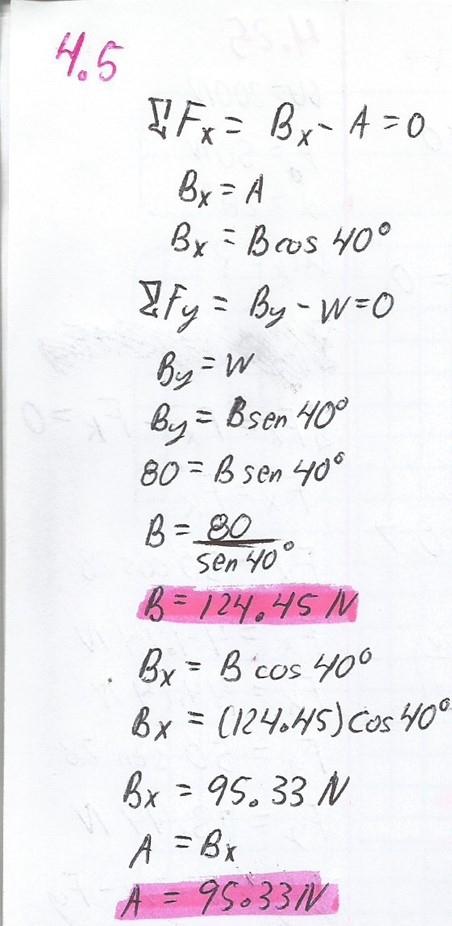
4.6.
Si la cuerda B en la figura 4.19a se rompe con tensiones mayores de 200 lb, ¿cuál es el peso máximo que W puede soportar?
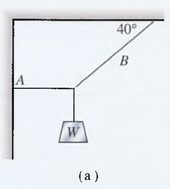
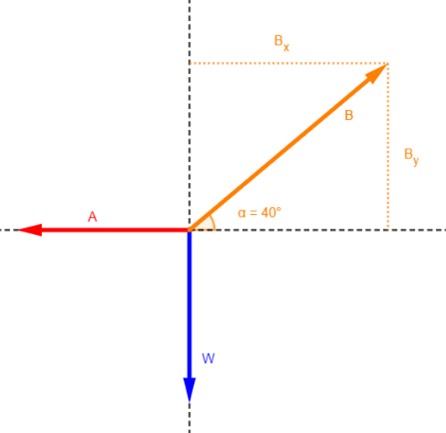

4.7.
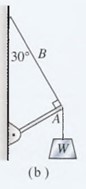
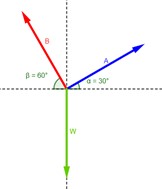
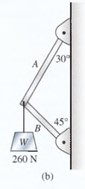
Si W = 600 N en la figura 4.19b, ¿cuál es la fuerza que ejerce la cuerda sobre el extremo de la vigueta A? ¿Cuál es la tensión en la cuerda B?

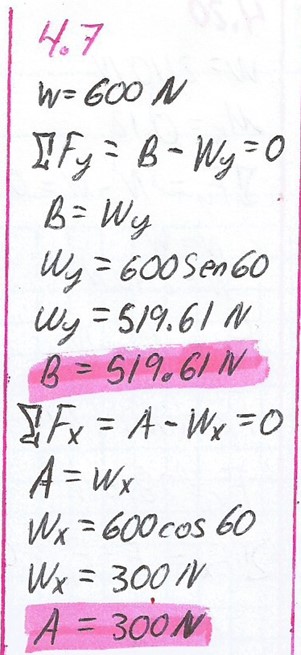
4.8.
La cuerda B de la figura 4.19a se rompe si su tensión excede 400 N, ¿cuál es el peso máximo W?
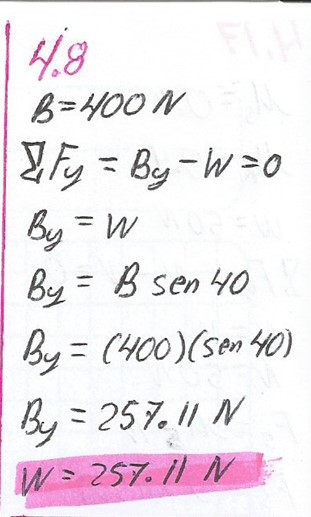
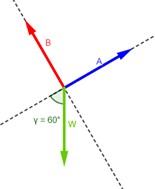
4.9.
¿Cuál es el peso máximo de W en el caso de la figura 4.19b si la cuerda solo puede soportar una tensión máxima de 800 N? (B = 800 N).
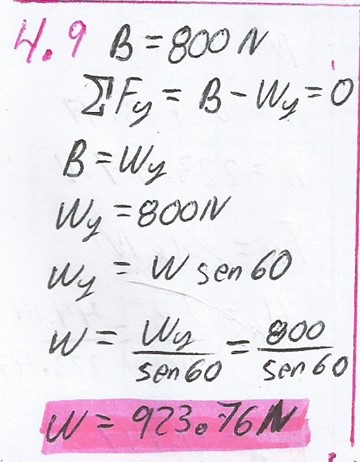
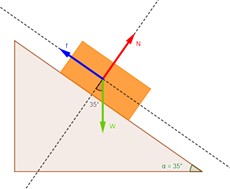
4.10.
Un bloque de 70 N reposa sobre un plano inclinado a 350. Calcule la fuerza normal y halle la fuerza de fricción por la que el bloque no resbala.

4.11.
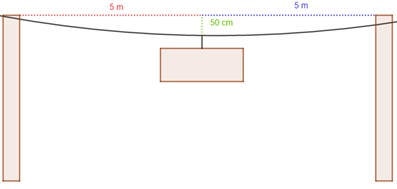
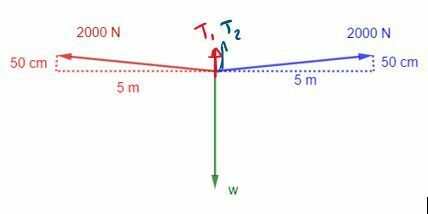
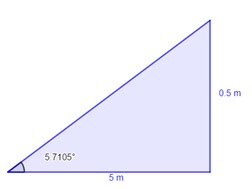
Un cable tendido sobre dos postes colocados con una separación de 10 m. A la mitad del cable se cuelga un letrero que provoca un pandeo, por lo cual el cable desciende verticalmente una distancia de 50 cm. Si la tensión en cada segmento del cable es de 2000 N, ¿Cuál es el peso del letrero?

4.12.
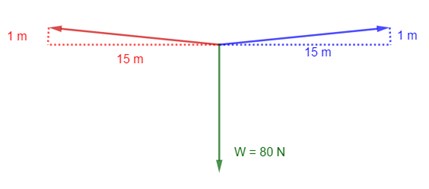
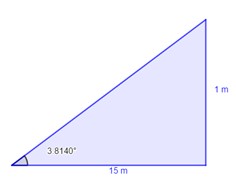
Un semáforo de 80 N cuelga del punto medio de un cable de 30 m tendido entre dos postes. Halle la tensión en cada segmento del cable si éste tiene un pandeo que lo hace descender una distancia vertical de 1 m.

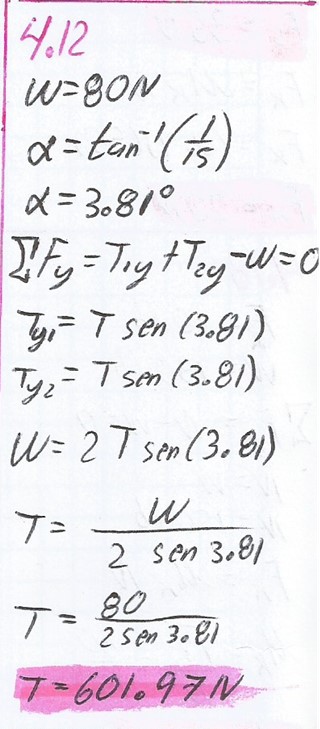
4.13.
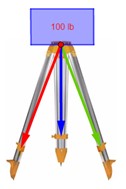
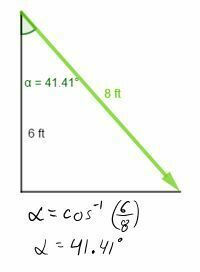
Los extremos de tres vigas de 8 ft están clavados unos con otros, formando así un trípode cuyo vértice se encuentra a una altura de 6 ft sobre el suelo. ¿Cuál es la compresión producida en cada uno cuando un peso de 100 lb se suspende de dicho vértice?
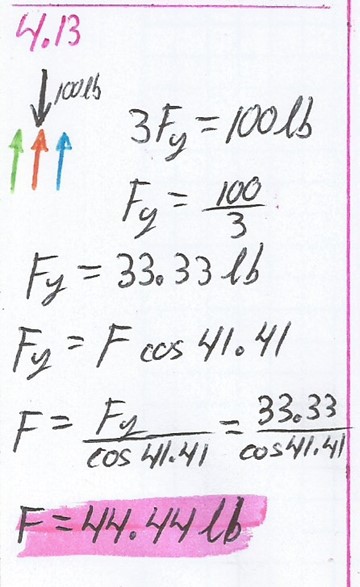
4.14.
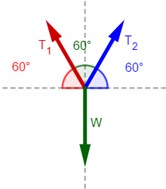
Un cuadro de 20 N se cuelga de un clavo, como indica la Figura 4.21, de manera que las cuerdas que lo sostienen forman un ángulo de 60º. ¿Cuál es la tensión en cada segmento de la cuerda?

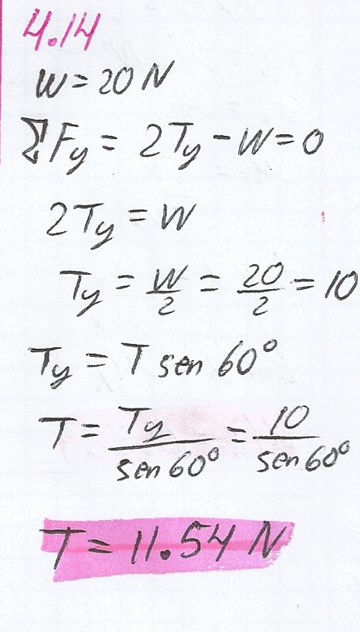
Fricción
4.15.
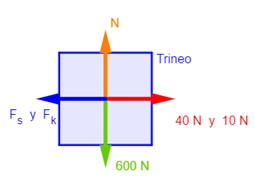
Una fuerza horizontal de 40 N apenas es suficiente para poner en marcha un trineo vacío de 600 N sobre nieve compacta. Después de empezar el movimiento se requieren tan sólo 10 N para mantener el trineo a rapidez constante. Halle los coeficientes de fricción estática y cinética.
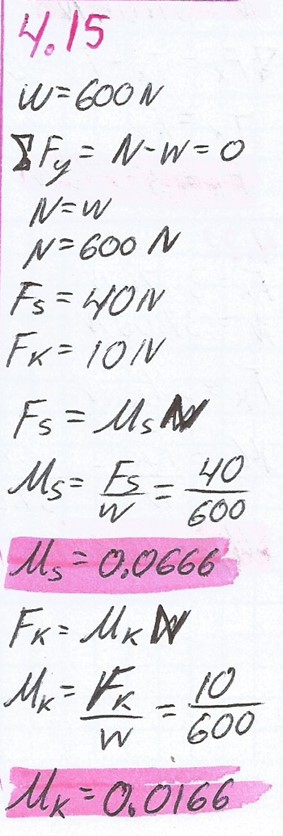
4.16.
Supongamos que en el trineo descrito en el problema anterior se colocaran 200 N de provisiones.
¿Cuál sería la nueva fuerza necesaria para arrastrarlo a rapidez constante?

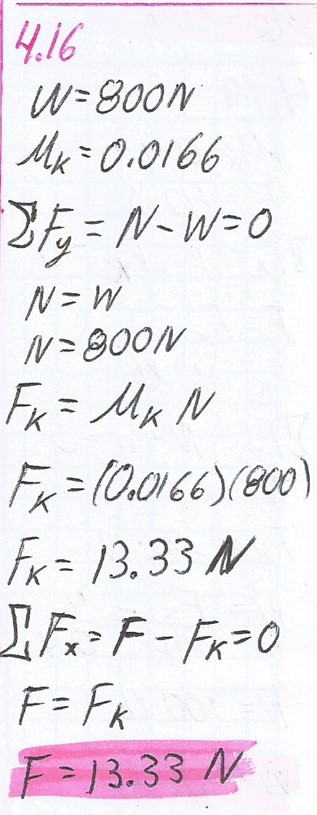
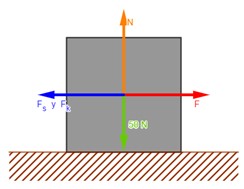
4.17.
Supongamos ciertas superficies en las que ms = 0.7 y mk = 0.4. ¿Qué fuerza horizontal se requiere para que un bloque de 50 N empiece a deslizarse sobre un piso de madera? ¿Qué fuerza se necesita para moverlo a rapidez constante?
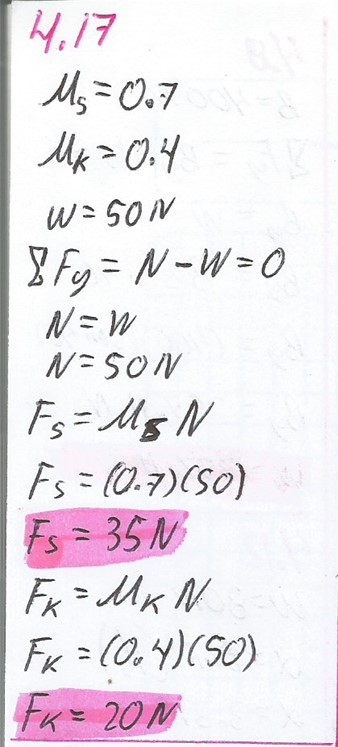
4.18.
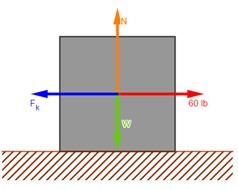
Un estibador se ha dado cuenta de que se requiere una fuerza horizontal de 60 lb para arrastrar una caja de 150 lb con rapidez constante sobre una plataforma de carga. ¿Cuál es el coeficiente de fricción cinética?
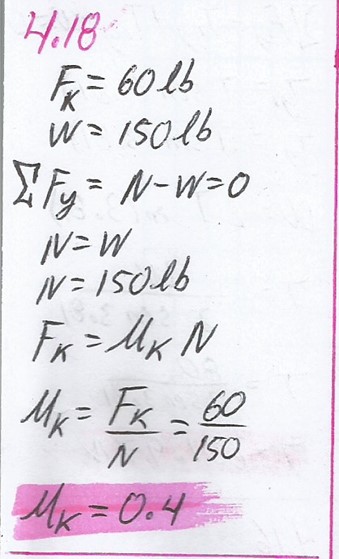
4.19.
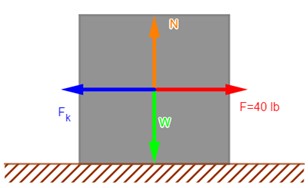
El estibador del problema 4.18 se percata de que una caja más pequeña del mismo material puede ser arrastrada con rapidez constante con una fuerza horizontal de sólo 40 lb. ¿Cuál es el peso de esta caja?
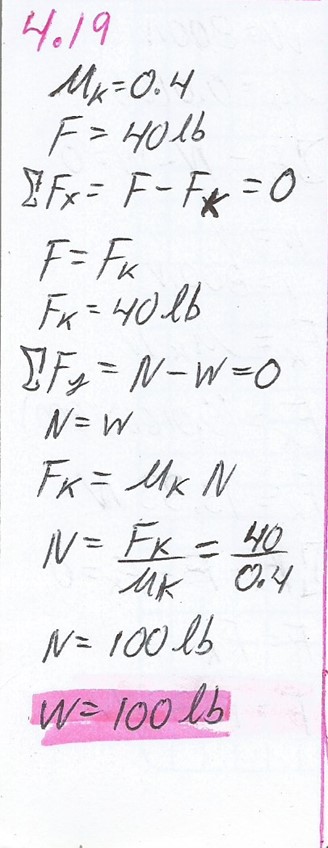
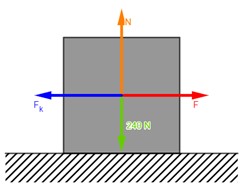
4.20.
Un bloque de acero que pesa 240 N descansa sobre una viga de acero nivelada. ¿Qué fuerza horizontal logrará mover el bloque a rapidez constante, si el coeficiente de fricción cinética es 0.12?
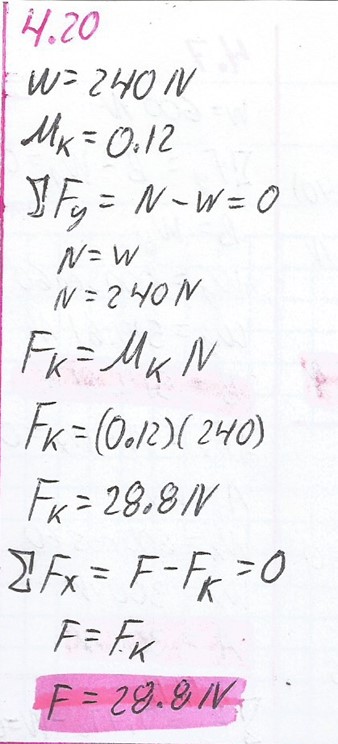
4.21.
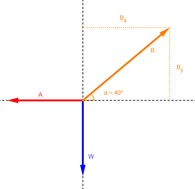
Una caja de herramientas de 60 N es arrastrada horizontalmente con una rapidez constante por medio de una cuerda que forma un ángulo de 35º con el piso. La tensión en la cuerda es de 40 N. Calcule las magnitudes de las fuerzas de fricción y de la fuerza normal.
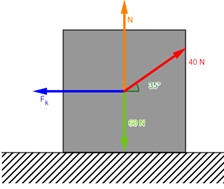
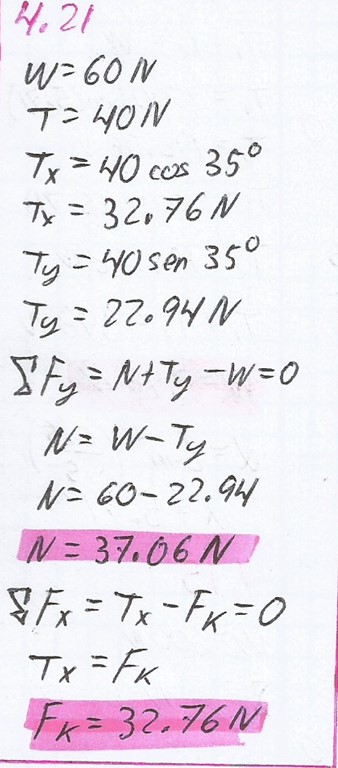
4.22.
¿Cuál es el coeficiente de fricción cinética en el ejemplo del problema 4.21?

4.23.
El coeficiente de fricción estática que corresponde a la madera sobre madera es de 0.7. ¿Cuál es el ángulo máximo que puede adoptar un plano inclinado de madera para que un bloque, también de madera, permanezca en reposo sobre el plano?
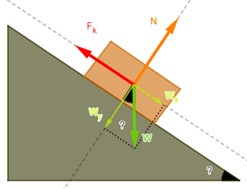

4.24.
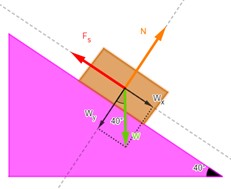
Un techo tiene una pendiente con un ángulo de 400. ¿Cuál debe ser el coeficiente máximo de fricción estática entre la suela de un zapato y ese techo para evitar que alguien resbale?
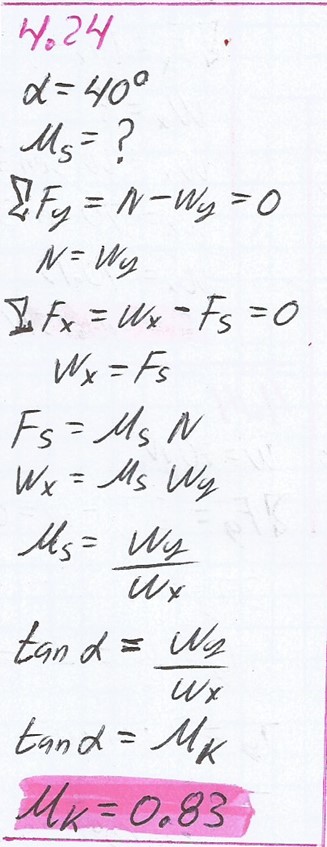
4.25.
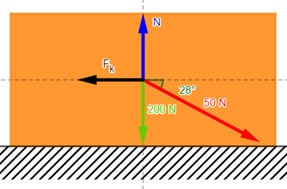
Se empuja un trineo de 200 N sobre una superficie horizontal a rapidez constante, por una fuerza de 50 N cuya dirección forma un ángulo de 28º por debajo de la horizontal.
¿Cuál es el coeficiente de fricción cinética en este caso?
[sociallocker id=”185″]
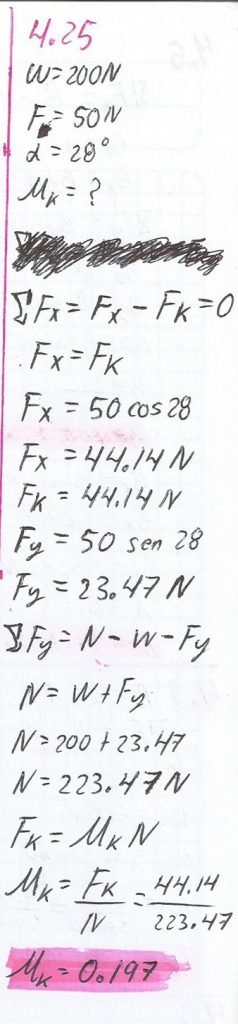
[/sociallocker]
4.26.
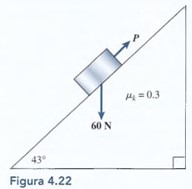
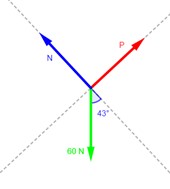
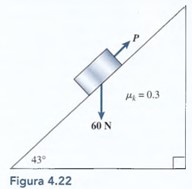
¿Cuál es la fuerza normal que actúa sobre el bloque en la Figura 4.22? ¿Cuál es la componente del peso que actúa hacia abajo del plano?
[sociallocker id=”185″]

[/sociallocker]
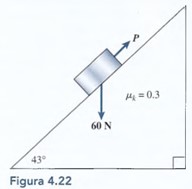
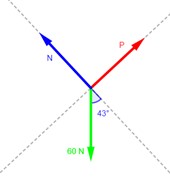
4.27.
¿Qué empuje P, dirigido hacia arriba del plano, hará que el bloque de la figura 4.22 suba por dicho plano con rapidez constante?
[sociallocker id=”185″]
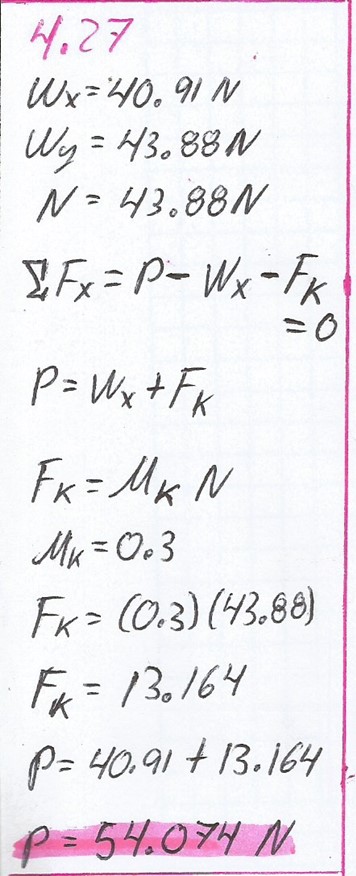
[/sociallocker]
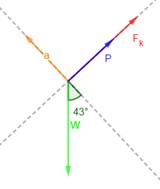
4.28.
Si el bloque de la figura 4.22 se suelta, logrará superar la fricción estática y se deslizará rápidamente descendiendo por el plano. ¿Qué empuje P, dirigido hacia la parte superior del plano inclinado, permitirá retardar el movimiento descendente hasta que el bloque se mueva con rapidez constante? (Note que F está ahora arriba del plano.)
[sociallocker id=”185″]
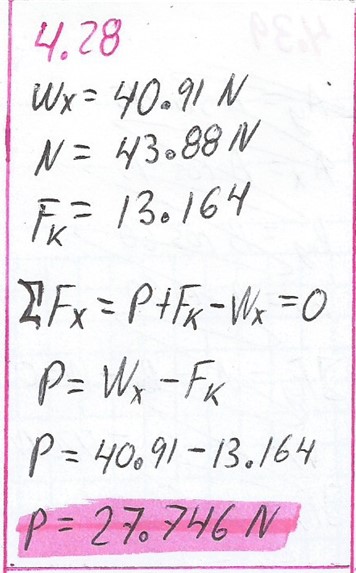
[/sociallocker]
Problemas adicionales
4.29.
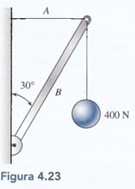
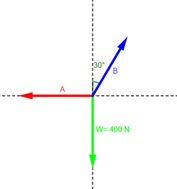
Calcule la tensión en la cuerda A y la fuerza B ejercida en la cuerda por la viga de la figura 4.23.
[sociallocker id=”185″]

[/sociallocker]
4.30.
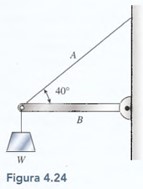
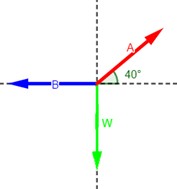
Si el cable A de la figura 4.24 tiene una resistencia a la rotura de 200 N, ¿cuál es el máximo peso que este aparato puede soportar?
[sociallocker id=”185″]
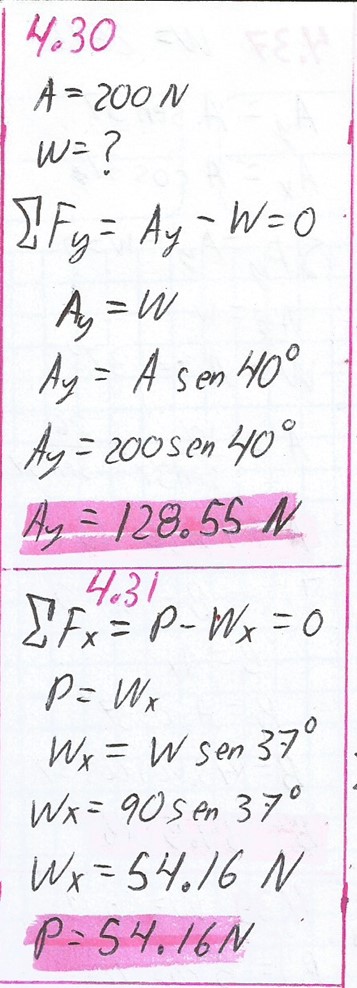
[/sociallocker]
4.31.
¿Cuál es el empuje mínimo P, paralelo a un plano inclinado de 37º, si un carrito de 90 N va a ascender por dicho plano con rapidez constante? Desprecie la fricción.
[sociallocker id=”185″]


[/sociallocker]
4.32.
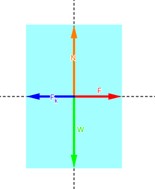
Una fuerza horizontal de sólo 8 lb mueve un trozo de hielo con rapidez constante sobre un piso (mk = 0.1). ¿Cuál es el peso del hielo?
[sociallocker id=”185″]
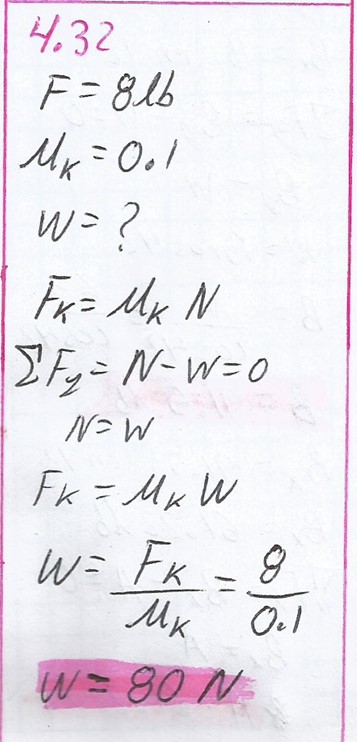
[/sociallocker]
4.33.
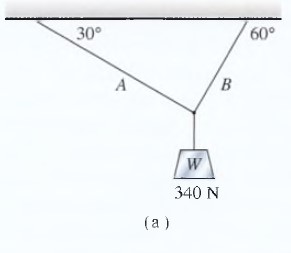
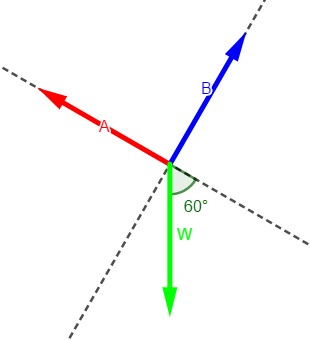
Encuentre la tensión en las cuerdas A y B en el dispositivo que muestra la figura 4.25a.
[sociallocker id=”185″]
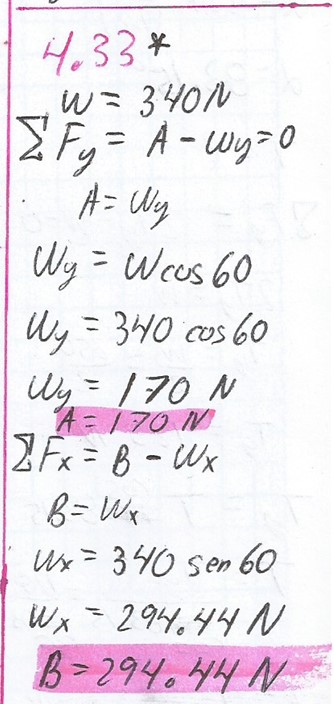
[/sociallocker]
4.34.
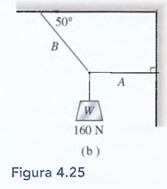
Calcule la tensión en las cuerdas A y B de la figura 4.25b.
[sociallocker id=”185″]

[/sociallocker]
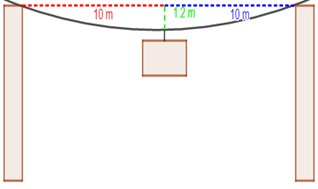
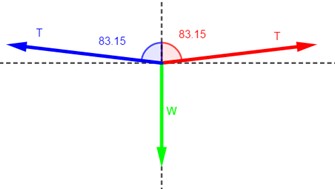
4.35.
Se ha tendido horizontalmente un cable en la punta de dos postes verticales colocados a 20 m de distancia uno del otro. Un letrero de 250 N está suspendido del punto medio del cable y hace que éste se pandee en una distancia vertical de 1.2 m. ¿Cuál es la tensión en cada uno de los segmentos del cable?
[sociallocker id=”185″]
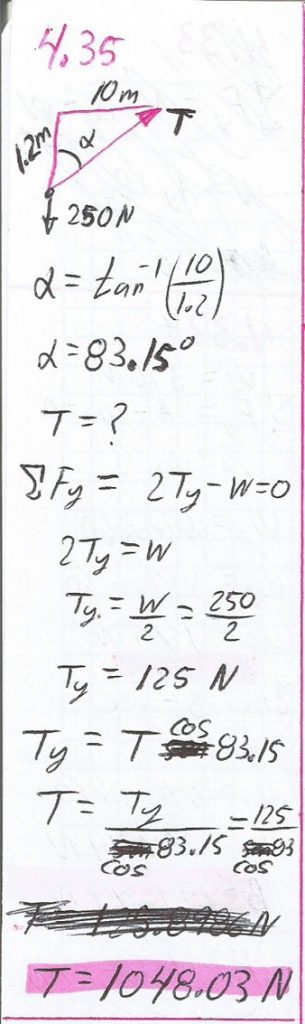
[/sociallocker]
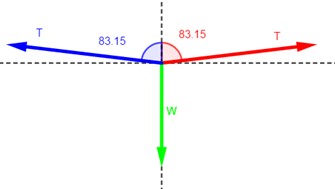
4.36.
Suponga que el cable del problema 4.35 tiene una resistencia a la rotura de 1200 N. ¿Cuál es el máximo peso que puede soportar en su punto medio?
[sociallocker id=”185″]
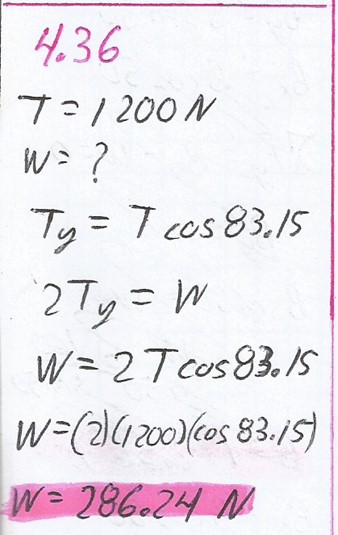
[/sociallocker]
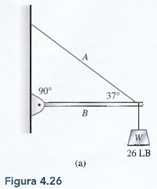
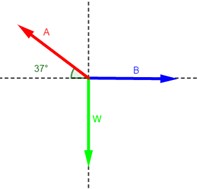
4.37.
Calcule la tensión en el cable y la compresión en la vigueta de la figura 4.26a.
[sociallocker id=”185″]
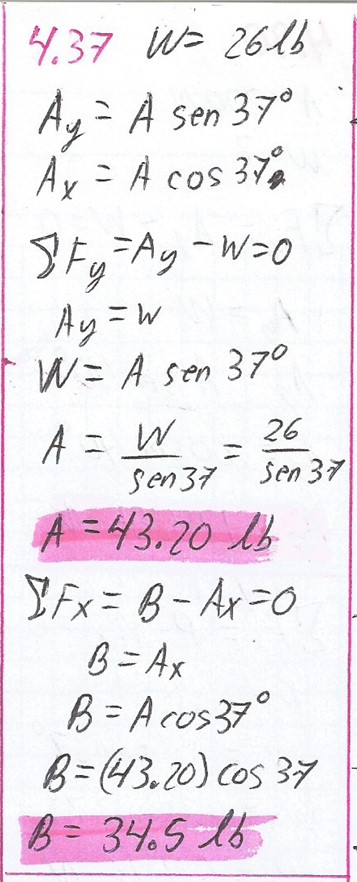
[/sociallocker]
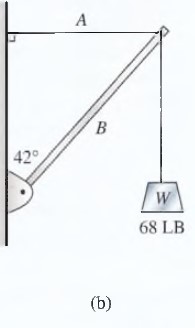
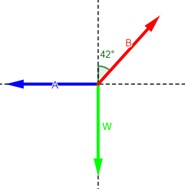
4.38.
Halle la tensión en el cable y la compresión en la vigueta de la figura 4.26b.
[sociallocker id=”185″]

[/sociallocker]
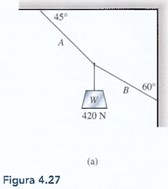
4.39.
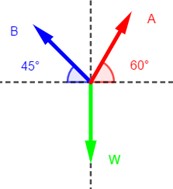
Calcule la tensión en las cuerdas A y B de la figura 4.27a.
[sociallocker id=”185″]
[/sociallocker]
4.40.
Halle las fuerzas en las tablas ligeras de la figura 4.27b e indique si éstas se encuentran bajo tensión o bajo compresión.
[sociallocker id=”185″]
[/sociallocker]

